Improve the sampling quality with the help of generative AI
Research ·To decipher how a biomolecular interacts with the environment, just knowing one of its static structures is not enough. Those biomolecules are adopting different poses in cells. An ensemble of these poses reveals more information about the system. In this project, we explore the possibility of using generative AI to generarte these poses.
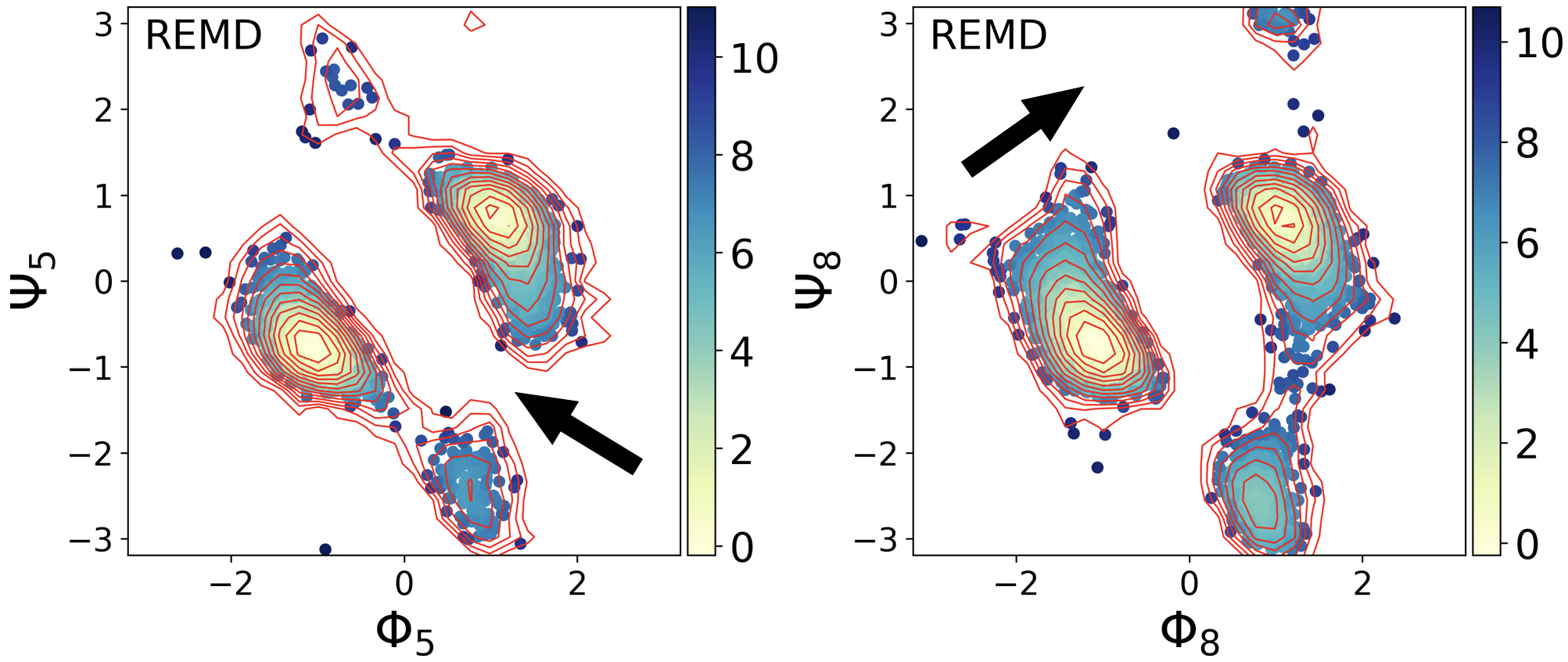
Of course, we can use a molecular dynamics (MD) simulation to generate different poses(states) of biomolecules. However, due to the sampling issue, the distribution of states may deviate from the equilibrium distribution. Even with the help of the enhanced sampling methods, this can still be a problem due to the limited computational resources. For example, as shown below, the states indicated by the black arrows were not sampled in a replica exchange molecular dynamics simulation. Though the simulation went to those states in higher temperature replicas, it is hard to use that information to tell us how those states should distribute at lower temperatures.
We use a recently developed generative AI model called the denoising diffusion probabilistic model to solve this problem. As illustrated by the figure below, the model is trained to reverse a forward diffusion process that starts with the target distribution and move towards an easy-to-sample distribution. The nice thing about such a design is that if we set the forward process to be the Ornstein–Uhlenbeck process, the diffusion kernel for the reversed process would also follow a Gaussian distribution, which can be easily learn by a neural network. With this model, we can generate samples from a complicated distribution by passing samples from the easy-to-sample distribution through the reverse process.

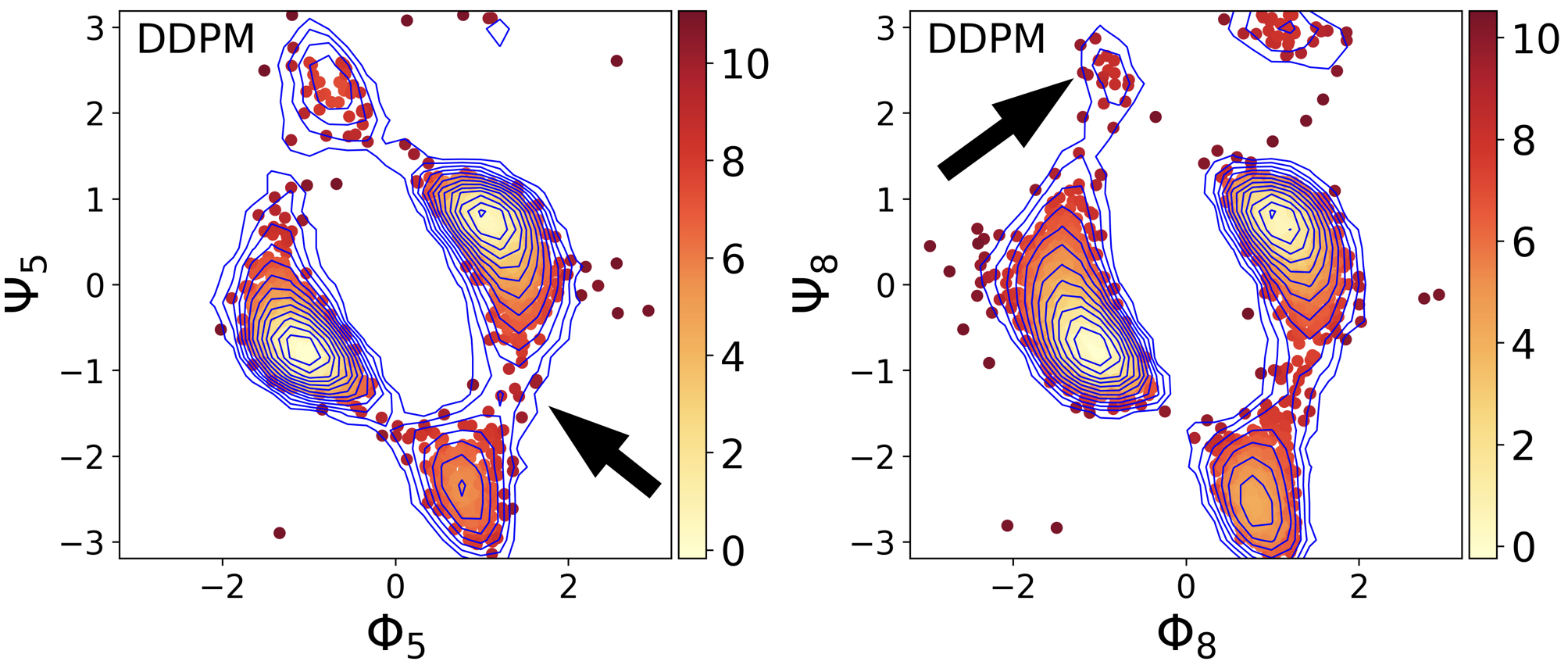
When applying this model to REMD data, we used it to learn the joint distribution $P(\mathbf{x}, T)$, where $\mathbf{x}$ denotes a state and $T$ is the temperature. This strategy allows the model to look at distribution at different temperatures and infer the underlying relationship. The figure below shows that the DDPM model can generate states that were not sampled in the simulation.
A full version of the paper can be found here.